Answer:
7.0625
Step-by-step explanation:
The trapezoidal rule ( this is an approximation ) tells you that the average of the left and right endpoints should be as follows,
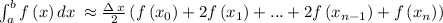
where
 ... at this point we can apply the Riemann Formula, in order to divide the interval 0 ≤ x ≤ 2 into n = 4 subintervals of length
... at this point we can apply the Riemann Formula, in order to divide the interval 0 ≤ x ≤ 2 into n = 4 subintervals of length
 .
.
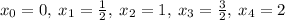 ,
,
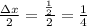
=
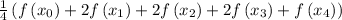 - Let's calculate the sub intervals for each, substituting to receive our solution.
- Let's calculate the sub intervals for each, substituting to receive our solution.
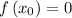 ( this is as 0⁴ is 0 )
( this is as 0⁴ is 0 )
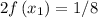 ( this is as
( this is as
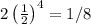 )
)
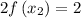 ( 2
( 2
 1⁴ is 2 )
1⁴ is 2 )
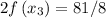 ( this is as
( this is as
 )
)
And finally
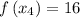 , as 2⁴ is 16. Therefore, let us plug in our solutions for each into the primary expression, and solve,
, as 2⁴ is 16. Therefore, let us plug in our solutions for each into the primary expression, and solve,
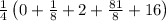 = 7.0625 - this is our solution. The correct answer is option c, and i hope this clarifies why.
= 7.0625 - this is our solution. The correct answer is option c, and i hope this clarifies why.