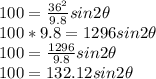Answer:
B.
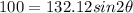
Explanation:
Given the horizontal distance in meters traveled by a projectile modeled by the function
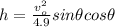 . If the initial velocity is 36 meters/second, the equation we would you use to find the angle needed to travel 100 meters is shown below;
. If the initial velocity is 36 meters/second, the equation we would you use to find the angle needed to travel 100 meters is shown below;
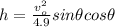
from trigonometry identity,
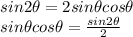
The equation will become;
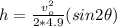
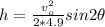
Given h = 100 meters and v = 36 m/s