Question

In a random sample of 40 refrigerators, the mean repair cost was $150. Assume the population standard deviation is $15.50. Construct a 99% confidence interval for the population mean repair cost. Then change the sample size to n = 60. Which confidence interval has the better estimate?

Answer 1

Answer: ($143.69, $156.31)

Explanation:

Confidence interval to estimate population mean :

`\overline{x}\ \pm z(\sigma)/(√(n))`

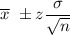
, where
`\sigma` = population standard deviation

n= sample size

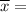`\overline{x}=` Sample mean

z= critical value.

As per given,

n= 40

`\sigma` = $15.50

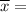`\overline{x}=` $150

Critical value for 99% confidence level = 2.576

Then, 99% confidence interval for the population mean:

`150\pm(2.576)(15.50)/(√(40))\\\\\Rightarrow\ 150\pm6.31 \ \ (approx)\\\\\Rightarrow(150-6.31,150+6.31)=(143.69,156.31)`

Hence, the required confidence interval : ($143.69, $156.31)