Question

Statistics students in Oxnard College sampled 10 textbooks in the Condor bookstore, and recorded number of pages in each textbook and its cost. The bivariate data is shown below, Number of Pages ( x ) Cost( y ) 526 52.08 625 59 589 56.12 409 25.72 489 34.12 500 53 906 78.48 251 26.08 595 50.6 719 68.52 A student calculates a linear model y = x + . (Please show your answers to two decimal places) Use the model above to estimate the cost when number of pages is 563 Cost = $ (Please show your answer to 2 decimal places.)

Answer 1

To estimate the cost of a textbook with 563 pages using the linear model y = x + c, substitute 563 for x and add the constant term c to the result.

Step-by-step explanation:

To estimate the cost of a textbook with 563 pages using the linear model, substitute 563 for x in the equation:

Cost = x + c

Since the coefficient for x is 1, we can simply add 563 to the constant term c:

Cost = 563 + c

Therefore, the estimated cost of the textbook with 563 pages is $563 + c.

Answer 2

y = -0.85 + 0.09x; $49.82

Step-by-step explanation:

1. Calculate Σx, Σy, Σxy, and Σx²

The calculation is tedious but not difficult.

`\begin{array}{rrrr}\mathbf{x} & \mathbf{y} & \mathbf{xy} & \mathbf{x^(2)}\\526 & 52.08 & 27394.08 & 276676\\625& 59.00 & 36875.00 &390625\\589 & 56.12 & 33054.68 & 346921\\409 & 25.72 & 10519.48 & 167281\\489 & 34.12& 16684.68 & 293121\\500 & 53.00 & 26500.00 &250000\\906 & 76.48 & 71102.88 & 820836\\251 &26.08 & 6546.08 & 63001\\595 & 50.60 & 30107.00 & 354025\\719 & 68.52 & 49265.88 & 516961\\\mathbf{5609} & \mathbf{503.72} &\mathbf{308049.76} & \mathbf{3425447}\\\end{array}`

2. Calculate the coefficients in the regression equation

`a = (\sum y \sum x^(2) - \sum x \sum xy)/(n\sum x^(2)- \left (\sum x\right )^(2)) = (503.7 * 3425447 - 5609 * 308049.76)/(10 * 3425447- 5609^(2))\\\\= (1725466163 - 1727851103.84)/(34254470 - 31460881) = -(2384941)/(2793589)= \mathbf{-0.8537}`

`b = (n\sumx y - \sum x \sumxy)/(n\sum x^(2)- \left (\sum x\right )^(2)) = (3080498 - 2825365.48)/(2793589) = (255132)/(2793589) = \mathbf{0.09133}`

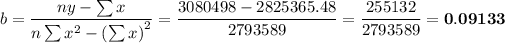
To two decimal places, the regression equation is

y = -0.85 + 0.09x

3. Prediction

If x = 563,

y = -0.85 + 0.09x = -0.85 + 0.09 × 563 = -0.85 + 50.67 = $49.82

(If we don't round the regression equation to two decimal places, the predicted value is $50.56.)