Question

A wave travels at 295 m/s and has a wavelength of 2.50 m. What is the frequency of the wave?

O 118 Hz
O 292 Hz
O297 Hz
O 738 Hz

Answer 1

118

Step-by-step explanation:

Answer 2

`118\; \rm Hz`.

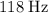Step-by-step explanation:

The frequency
`f` of a wave is equal to the number of wave cycles that go through a point on its path in unit time (where "unit time" is typically equal to one second.)

The wave in this question travels at a speed of
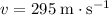`v= 295\; \rm m\cdot s^(-1)`. In other words, the wave would have traveled
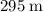`295\; \rm m` in each second. Consider a point on the path of this wave. If a peak was initially at that point, in one second that peak would be

How many wave cycles can fit into that
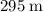`295\; \rm m`? The wavelength of this wave
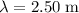`\lambda = 2.50\; \rm m` gives the length of one wave cycle. Therefore:

`\displaystyle (295\;\rm m)/(2.50\; \rm m) = 118`.

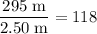That is: there are
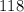`118` wave cycles in
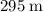`295\; \rm m` of this wave.

On the other hand, Because that
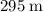`295\; \rm m` of this wave goes through that point in each second, that
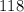`118` wave cycles will go through that point in the same amount of time. Hence, the frequency of this wave would be

Because one wave cycle per second is equivalent to one Hertz, the frequency of this wave can be written as:

`f = 118\; \rm s^(-1) = 118\; \rm Hz`.

The calculations above can be expressed with the formula:

`\displaystyle f = (v)/(\lambda)`,

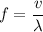where

• 
  `v` represents the speed of this wave, and
• 
  `\lambda` represents the wavelength of this wave.