Question

A company sells widgets. The amount of profit, y, made by the company, is related to the selling price of each widget, x, by the given equation. Using this equation, find out what price the widgets should be sold for the company to make the maximum profit. y=-10x^2+689x-6775 The selling price should be $

Answer 1

x = $34.45

Step-by-step explanation:

Solution:-

The company makes a profit of $y by selling widgets at a price of $x. The profit model is represented by a parabola ( quadratic ) equation as follows:

`y = -10x^2 + 689x -6775`

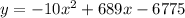
We are to determine the profit maximizing selling price ( x )

From the properties of a parabola equation of the form:

`y = ax^2 + bx + c`

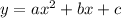
The vertex ( turning point ) or maximum/minimum point is given as:

`x = -(b)/(2a) \\\\x = - (689)/(2*(-10)) = (689)/(20)\\\\x = 34.45`

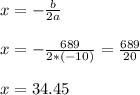
The profit maximizing selling price of widgets would be x = $34.45.