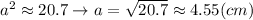Question

A solid square pyramid has a mass of 750 g. It is made of a material with a

density of 8.05 g/cm'. Given that the height of the pyramid is 13.5 cm, find the
length of its square base.​

Answer 1

Explanation:

volume of pyramid=1/3×base area×height

let the length of base=x

base area=x²

volume V=1/3×x²×13.5=4.5 x²

mass=volume×density

750=4.5 x²×8.05=36.225 x²

x²=750/36.225

x=√(750/36.225)≈4.55 cm

Answer 2

4.55cm

Explanation:

The unit of a volume:
`cm^3`

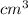
The unit of a density:
`(g)/(cm^3)`

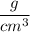
The density is
`(mass)/(volume)`

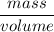
Substitute:

`(8.05g)/(cm^3)=(750g)/(V)`

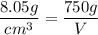
cross multiply

`8.05gV=750gcm^3`

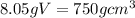
divide both sides by 8.05g

`V\approx93.17cm^3`

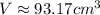
The formula of a volume of a square pyramid:

`V=(1)/(3)a^2H`

a - length of square base

H - height of a pyramid

We have:

`V=93.17cm^3;\ H=13.5cm`

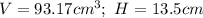
Substitute:

`93.17=(1)/(3)a^2(13.5)`

multiply both sides by 3

`279.51=13.5H`

`297.51=13.5a^2`

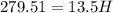
divide both sides by 13.5

`a^2\approx20.7\to a=√(20.7)\approx4.55(cm)`