Question

An economist is studying the linear relationship between the selling price p, of a

mobile phone and the number of persons buying the phone x. The table of values
illustrates her findings. Write the equation that represents the relationship between the
number of persons buying the phone and the price of the phone.​

Answer 1

The equation that represents the number of persons buying the phone and the price of the phone is y = -0.75·x + 60

Explanation:

The given data are as follows

x, p($)

10, 52.5

25, 41.25

40, 30

60, 15

We note that a plot of the given points give a straight line graph indicating a linear relationship

The rate of change of p($) with x is given by slope, m in the following relation;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

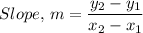
Which gives;

`Slope, \, m =(41.25-52.5)/(25-10) = (30-41.25)/(40-25) = (15-30)/(40-60) =-0.75`

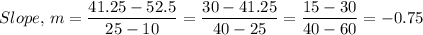
Therefore, to write the equation in slope and intercept form, we have;

From the first point with coordinates (52.5, 10), we have

y - 52.5 = -0.75×(x - 10)

y = -0.75·x + 7.5 + 52.5 = -0.75·x + 60

The equation that represents the number of persons buying the phone and the price of the phone is y = -0.75·x + 60.