Question

The function f is defined as follows.

f(x) =4x²+6
If the graph of f is translated vertically upward by 4 units, It becomes the graph of a function g.
Find the expression for g(x).


G(x)=

Answer 1

`g(x)=4x^(2) +10`

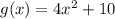
Explanation:

If we perform a vertical translation of a function, the graph will move from one point to another certain point in the direction of the y-axis, in another words: up or down.

Let:

`a>0,\hspace{10}a\in R`

For:

• y = f (x) + a: The graph shifts a units up.
• y = f (x) - a, The graph shifts a units down.

If:

`f(x)=4x^(2) +6`

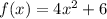
and is translated vertically upward by 4 units, this means:

`a=4`

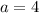
and:

`g(x)=f(x)+a=(4x^(2) +6)+4=4x^(2) +10`

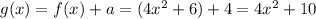
Therefore:

`g(x)=4x^(2) +10`

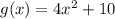
I attached you the graphs, so you can verify the result easily.