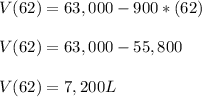Answer:
a. -900 L/min
b. Vo = 63,000 Liters
c. V ( t ) = 63,000 - 900*t
d. 7,200 Liters
Explanation:
Solution:-
We have a swimming pool which is drained at a constant linear rate. Certain readings were taken for the volume of water remaining in the pool ( V ) at different instances time ( t ) as follows.
t = 20 mins , V = 45,000 Liters
t = 70 mins , V = 0 Liters
To determine the rate ( m ) at which water drains from the pool. We can use the linear rate formulation as follows:
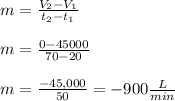
We can form a linear relationship between the volume ( V ) remaining in the swimming pool at time ( t ), using slope-intercept form of linear equation as follows:
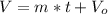
Where,
m: the rate at which water drains
Vo: the initial volume in the pool at time t = 0.
We can use either of the data point given to determine the initial amount of volume ( Vo ) in the pool.
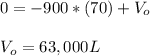
We can now completely express the relationship between the amount of volume ( V ) remaining in the pool at time ( t ) as follows:
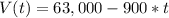
We can use the above relation to determine the amount of volume left after t = 62 minutes as follows: