Question

Different cereals are randomly selected and the sugar content in grams of sugar per grams of cereal are obtained. Use a .05 significance level to test the claim of cereal lobbyist that the mean sugar content for all cereals is less than .3 g. Data set: 0.03, 0.24, 0.30, 0.47, 0.43, 0.07, 0.47, 0.13, 0.44, 0.39, 0.48, 0.17, 0.13, 0.09, 0.45, 0.43

Answer 1

Explanation:

Hello!

X: content of sugar of a sample of cereal.

Data set:

0.03, 0.24, 0.30, 0.47, 0.43, 0.07, 0.47, 0.13, 0.44, 0.39, 0.48, 0.17, 0.13, 0.09, 0.45, 0.43

n= 16

`\frac{}{X}`= 0.295g

S= 0.17g

You have to test if the mean sugar content is less than 0.3g

H₀: μ ≥ 0.3

H₁: μ < 0.3

α: 0.05

Assuming that the variable has a normal distribution, you have to conduct a t test:

`t= \frac{\frac{}{X}-Mu }{(S)/(√(n) ) } ~~t_(n-1)`

`t_(H_0)= (0.295-0.30)/((0.17)/(√(16) ) ) = -0.12`

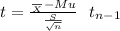
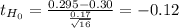
p-value: 0.4533

The p-value is greater than α, the decision is to not reject the null hypothesis.

At a 5% significance level the decision is to not reject the null hypothesis. You can conclude that the average sugar content of the cereal is equal or greater than 0.3g of sugar per gram of cereal.

I hope this helps!