Answer:
Explanation:
Hello!
You have to determine the sample size to take to estimate the population proportion of Democrats among registered voters in Texas for a 96% interval with a margin of error of 0.01 and sample proportion p'= 0.28
The interval for the population proportion is
p' ±
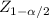 *
*
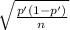
The margin of error of the interval is:
d=
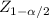 *
*
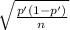
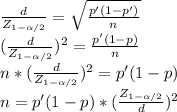
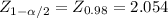
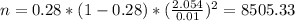
n= 8506 voters
I hope this helps!