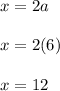Question

Find the value of x in the isoscleles triangle sqrt45 and altitude 3​

Answer 1

`c.\hspace{3}x=12`

Explanation:

Isosceles triangles are a type of triangles in which two of their sides have an identical length. It should be noted that the angles opposite the sides that are the same length are also the same. This means that these triangles not only have two equal sides, but also two equal angles.

You can solve this problem using different methods, I will use pythagorean theorem. First take a look at the picture I attached. As you can see:

`x=2a`

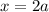
And we can find a easily using pythagorean theorem:

`(√(45) )^(2) =3^(2) +a^(2)`

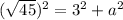
Solving for a:

`a^(2) =(√(45) )^(2) -3^(2) \\\\a^(2) =45-9\\\\`

`a^(2) =36\\\\a=√(36) \\\\a=6`

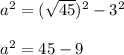
Therefore:

`x=2a\\\\x=2(6)\\\\x=12`