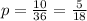Question

A standard dice is tossed twice. What is the probability of obtaining exactly one 5? Express your answer as a common fraction.

Answer 1

S= (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

For this case the size of the sample space is 36 now we count the number of pairs with exactly one 5 and we have:

(1,5), (2,5), (3,5), (4,5), (6,5), (5,6), (5,4), (5,3), (5,2), (5,1)

And then the probability would be:

`p=(10)/(36)= (5)/(18)`

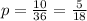
Explanation:

For this case w ehave the following sample space:

S= (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

For this case the size of the sample space is 36 now we count the number of pairs with exactly one 5 and we have:

(1,5), (2,5), (3,5), (4,5), (6,5), (5,6), (5,4), (5,3), (5,2), (5,1)

And then the probability would be:

`p=(10)/(36)= (5)/(18)`

Answer 2

5/18

Explanation:

There are a couple of ways to look at this.

1) If you make a matrix of all possibilities, you find there are 36 possible outcomes from the roll of a die twice. (That is the same number as for rolling two dice once.) Of those 36 outcomes, 10 are outcomes in which a 5 shows exactly once: (5, 1), (5, 2), (5, 3), (5, 4), (5, 6), (1, 5), (2, 5), (3, 5), (4, 5), (6, 5).

The probability of obtaining exactly one 5 is 10/36 = 5/18.

__

2) As listed above, there are two ways to get exactly one 5 in two rolls:

(5 on the first, non-5 on the second) or (non-5 on the first, 5 on the second)

When the rolls are independent, as we assume here, the probability of a certain sequence is the product of the probabilities of the events in that sequence.

P(5, non-5) = (1/6)(5/6) = 5/36

P(non-5, 5) = (5/6)(1/6) = 5/36

The probability of obtaining either event is the sum of their individual probabilities:

P({5, 5'} or {5', 5}) = 5/36 +5/36 = 10/36 = 5/18

__

The probability of obtaining exactly one 5 in two rolls of a die is 5/18.