Question

How does the frequency of f(x) = cos(2x) relate to the frequency of the parent function cos x?

Answer 1

The frequency of f(x) is two times the frequency of the parent function.

Explanation:

We can say that the number that is beside the x is equal to
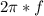`2\pi *f`, where f is the frequency.

Then, for the parent function, we get:

`1 = 2\pi f_1`

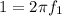
or solving for
`f_1`:

`f_1=(1)/(2\pi )`

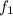At the same way, for f(x), we get:

`2=2\pi f_2\\f_2=2((1)/(2\pi ))`

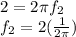
But
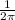`(1)/(2\pi )` is equal to
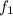`f_1`, so we can write the last equation as:

`f_2=2f_1`

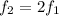
It means that the frequency of f(x) is two times the frequency of the parent function.