Question

The graphed line shown below is y = negative 2 x minus 8. Which equation, when graphed with the given equation, will form a system that has infinitely many solutions? y = negative (2 x + 8) y = negative 2 (x minus 8) y = negative 2 (x minus 4) y = negative (negative 2 x + 8)

Answer 1

`\boxed{y = -(2x + 8)}`

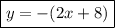
Explanation:

For the two lines to have infinite
`\infty` solutions, the two equations must be the same.

First equation : y = -2x - 8

A. y = -(2x + 8)

y = -2x - 8 correct

B. y = -2(x - 8)

y = -2x + 16 incorrect

C. y = -2(x - 4)

y = -2x + 8 incorrect

D. y = -(-2x+8)

y = 2x - 8 incorrect

y = -2x - 8 and y = -(2x + 8) when graphed are the same, they intersect at infinite points and there are infinite solutions.

Answer 2

Answer: A y = -(2x+8)

Explanation:

The first line is y=-2x-8

Thus, the answer that simplifies to y = -2x-8 is the answer.

a) y=-(2x+8)

Distribute

y=-2x-8

Because it works, no need to try the others.

Hope it helps <3