A. Depending on which variable you choose to integrate with, you can capture the total bounded region with either -2 ≤ x ≤ (-1 + √5)/2 or 1 ≤ y ≤ (5 + √5)/2, where the upper endpoints correspond to the coordinates of the appropriate intersections:
y = x² + 1
⇒ x = (x² - 2)² - 2
⇒ x⁴ - 4x² - x + 2 = 0
⇒ (x - 2) (x + 1) (x² + x - 1) = 0
⇒ x = 2, x = -1, x = -1/2 ± √5/2
⇒ y = 5, y = 2, y = (5 ± √5)/2
On the other hand, we can compute the areas of A and B separately, then sum those integrals. Area A is easier to compute by integrating with respect to y over 2 ≤ y ≤ (5 + √5)/2, while area B is easier to find by integrating x over -1 ≤ x ≤ (-1 + √5)/2.
B. I'll stick to the split-region approach.
First, we find equations for the appropriates halves of either parabola:
• y = x² + 1 ⇒ x = ± √(y - 1)
and x = -√(y - 1) describes the left half of the blue parabola;
• x = (y - 3)² - 2 ⇒ y = 3 ± √(x + 2)
and y = 3 - √(x + 2) describe the bottom half of the red parabola.
Now we can set up the integrals.
Area of A:
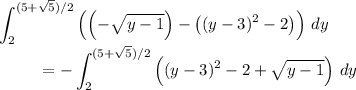
Area of B:
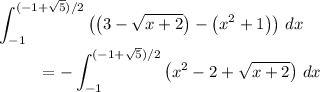
Alternatively, one can prove that the regions A and B are symmetric across the line y = x + 3, so we can simply pick one of these integrals and double it.
C. Computing the integrals, we find
area of A = 2/3
area of B = 2/3
and so the total area is 2/3 + 2/3 = 4/3.