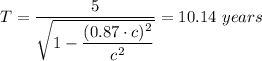Question

Explain length and time dilation and give an example of when each is observed.

Answer 1

Length contraction

A moving object traveling at a velocity approaching the speed of light will appear to be shorter or to have undergone contraction.

The proportion by which the object is observed to have contracted is given by Lorentz transformation as follows;

`L = L_(0)\cdot \sqrt{1 -(v^(2))/(c^(2))}= (L_(0))/(\gamma )`

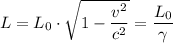
Time dilation

As the relative speed of motion of an object approaches the speed of light, the clock in the frame in motion will be observed to be moving slowly or dilated in a proportion given by Lorentz transformation as follows;

`T = \frac{T_(0)}{\sqrt{1 -(v^(2))/(c^(2))}}`

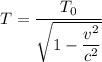
Step-by-step explanation:

Example of length contraction example

Two square boxes of side length L which are travelling at a velocity of 0.9 × c, are going to arranged in a single box of side side length L according to length contraction Lorentz transformation, to stationary observer we have

`2 * L\cdot \sqrt{1 -((0.9 \cdot c)^(2))/(c^(2))}= 0.8 \cdot L`

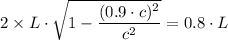
To the stationary observer, the 2 boxes of length L will fit side by side in the single box of length L, while to those on the space ship carrying the boxes, the size of the single box is
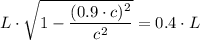`L\cdot \sqrt{1 -((0.9 \cdot c)^(2))/(c^(2))}= 0.4 \cdot L`, which will not contain half of one box

Example of of time dilation example

Twin A of two twins, twin A and B went on a space journey at the speed of 0.87·c for 5 years, the number of years past for twin B when they meet again will be
`T = \frac{5}{\sqrt{1 -((0.87\cdot c)^(2))/(c^(2))}} = 10.14 \ years`