Question

To dilute a solution that is 40% saline, a chemist combines it with a solution that is 15% saline. How much of each solution should she use if she needs 150 mL of a solution that is 25% saline? Hint: solve by using system of equations

Answer 1

`37.5= 0.4 x +0.15 y`

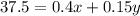
We can solve for x and we got:

`x= (37.5-0.15y)/(0.4)= 93.75-0.375 y`

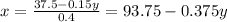
And replacing into the water condition we have:

`112.5 = (93.75-0.375 y)*0.6 +0.85y`

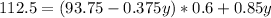
Solving for y we got:

`112.5= 56.25 -0.225 y+0.85 y`

`y = (112.5-56.25)/(0.625)= 90`

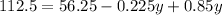
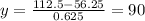
And then solving for x we got:

`x=(37.5- 0.15*90)/(0.4)= 60`

So we need 60 ml for the solution of 40% saline and 90 ml for the 15% saline solution

Explanation:

We can solve this problem with the following system of equations:

`150*0.25 = x*0.4 + y *0.15` salt

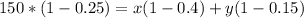`150*(1-0.25)= x(1-0.4) +y(1-0.15)` water

With x the ml of solution for 40% concentration and y the ml of solution at 15% of concentration

From the salt condition we have:

`37.5= 0.4 x +0.15 y`

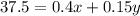
We can solve for x and we got:

`x= (37.5-0.15y)/(0.4)= 93.75-0.375 y`

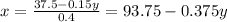
And replacing into the water condition we have:

`112.5 = (93.75-0.375 y)*0.6 +0.85y`

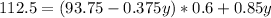
Solving for y we got:

`112.5= 56.25 -0.225 y+0.85 y`

`y = (112.5-56.25)/(0.625)= 90`

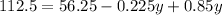
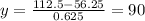
And then solving for x we got:

`x=(37.5- 0.15*90)/(0.4)= 60`

So we need 60 ml for the solution of 40% saline and 90 ml for the 15% saline solution

Answer 2

60 ml of 40% saline and 90 ml of 15% saline

Explanation:

We can call the amount of 40% solution x and the amount of 15% solution y.

x + y = 150 -- (1)

0.40x + 0.15y = 150 * 0.25 -- (2) --- 150 * 0.25 = 37.5

40x + 15y = 3750 (Multiply (2) by 100 to get rid of decimals)

15x + 15y = 2250 -- (3) (Multiply (1) by 15)

25x = 1500 (Subtract (3) from (1)

x = 60

y = 150 - 60 = 90