Question

Biologists stock a lake with 160

160
fish, and estimate the carrying capacity of the lake to be 9100
9100
fish. The number of fish tripled in the first year.
(a) Assuming that the fish population satisfies logistic growth, the fish population can be modeled by:()=/[1+55.875−1.13506]

From the given information about this population, determine the constant
that completes the model.

Answer 1

`P ( t ) = (9100.024)/(1 + 55.875e^-^1^.^1^3^5^0^6^*^t)`

Explanation:

Solution:-

- We are given a logistic growth model of the fish population cultured. The logistic growth of fish population is modeled by the following equation:

`P ( t ) = (c)/(1 + 55.875e^-^ 1^.^1^3^5^0^6^t)`

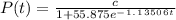
Where, c: the constant to be evaluated.

- We are given the initial conditions for the model where at t = 0. The initial population was given to be:

t = 0 , Po = 160

N ( carrying capacity ) = 9100

- After a year, t = 1. The population was tripled from the initial value. That is P ( 1 ) = Po*3 = 160*3 = 480.

- We will use the given logistic model and set P ( 1 ) = 480 and determine the constant ( c ) as follows:

`P ( 1 ) = (c)/(1 + 55.875e^-^ 1^.^1^3^5^0^6^*^1) = 480\\\\c = 480* [ 1 + 55.875e^-^ 1^.^1^3^5^0^6]\\\\c = 9100.024`

- The complete model can be written as:

`P ( t ) = (9100.024)/(1 + 55.875e^-^1^.^1^3^5^0^6^*^t)`