Question

Select the statements that are true for the graph of y=−(x−0.5)^2 +9 . Choose all correct statements. The vertex is (−0.5,9) . The graph has a maximum. The graph has a minimum. The vertex is ​ (0.5,9) ​.

Answer 1

1. the vertex is (0.5, 9)

2. it has a maximum.

Answer 2

The second and fourth statements are correct.

Explanation:

We are given the function for the graph of:

`y=-(x-0.5)^2+9`

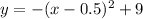
Note that this is a quadratic function in its vertex form, given by:

`y=a(x-h)^2+k`

Where a is the leading coefficient and (h, k) is the vertex.

Rewriting our given equation yields:

`\displaystyle y = (-1)(x-(0.5))^2 + (9)`

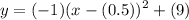
Therefore, a = -1, h = 0.5, and k = 9.

Therefore, the vertex of the graph is at (0.5 ,9).

Because the leading coefficient is negative, the parabola opens downwards.

Therefore, the parabola has a maximum value.

In conclusion, the second and fourth statements are correct.