Answer:
For this case a polynomial is defined with the following expression:
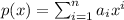 For all x on the domain considered and n is finite
For all x on the domain considered and n is finite
And by definition the absolute value function is defined as:
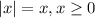
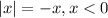
If we use the function
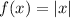 we see that is impossible to obtain the general expression of a polynomial since we can't obtain the form |x| and since we don't satisfy the definition the answer would be:
we see that is impossible to obtain the general expression of a polynomial since we can't obtain the form |x| and since we don't satisfy the definition the answer would be:
An absolute value function CANNOT be considered as a polynomial function
Explanation:
For this case a polynomial is defined with the following expression:
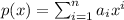 For all x on the domain considered and n is finite
For all x on the domain considered and n is finite
And by definition the absolute value function is defined as:
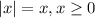
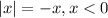
If we use the function
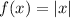 we see that is impossible to obtain the general expression of a polynomial since we can't obtain the form |x| and since we don't satisfy the definition the answer would be:
we see that is impossible to obtain the general expression of a polynomial since we can't obtain the form |x| and since we don't satisfy the definition the answer would be:
An absolute value function CANNOT be considered as a polynomial function