Question

10.Given the following, including the fact

that ∠ABC and ∠CBD are supplementary,
what is the value of m ∠ABC and m ∠ABC?
m ∠DBC=x−10
m ∠ABC=x+30.

Answer 1

m ∠DBC=80−10=70

m ∠ABC=80+30=110

Explanation:

m ∠DBC+m ∠ABC=180

( x−10)+(x+30.)=180

2x+20=180

2x=180-20

2x=160

x=80

>>m ∠DBC=80−10=70

>>m ∠ABC=80+30=110

Answer 2

`\boxed{<DBC = 70 degrees}\\\boxed{<ABC = 110 degrees}`

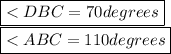
Explanation:

∠ABC and ∠DBC are supplementary which means that the sum of these two angles is equal to 180.

∠ABC + ∠DBC = 180

Given that: ∠ABC = x+30 and ∠DBC = x - 10

So,

=> x+30+x-10 = 180

=> 2x+20 = 180

=> 2x = 180-20

=> 2x = 160

Dividing both sides by 2

=> x = 80

Now, Finding measures of the angles.

=> ∠DBC = x-10 = 80-10 = 70 degrees

=> ∠ABC = x+30 =80+30 = 110 degrees