Question

Use the Factor Theorem to determine which of the following are NOT factors of 3x^4 - 5x^3 - 71 x^2 + 157x + 60 a. x - 3 c. x - 2/3 b. x + 1/3 d. x - 4

Answer 1

c. x - 2/3

Explanation:

The given equation is f(x) =
`3x^4 - 5x^3 - 71 x^2 + 157x + 60`

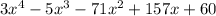
To test if the given equations are factors of the polynomial, check if the remainder is equal to zero if substituted into the equation.

For x - 3, x = 3

Substituting x = 3 into the given polynomial:

`f(3) = 3(3)^4 - 5(3)^3 - 71 (3)^2 + 157(3) + 60\\f(3) = 0`

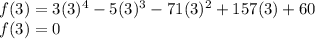
x - 3 is a factor

For x - 4, x = 4

Substituting x = 4 into the given polynomial:

`f(4) = 3(4)^4 - 5(4)^3 - 71 (4)^2 + 157(4) + 60\\f(4) = 0`

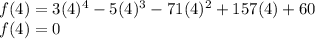
x - 4 is a factor

For x - 2/3, x = 2/3

Substituting x = 2/3 into the given polynomial:

`f(2/3) = 3(2/3)^4 - 5(2/3)^3 - 71 (2/3)^2 + 157(2/3) + 60\\f(2/3) = 132.22`

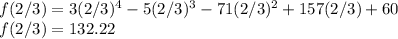
x - 2/3 is not a factor

For x + 1/3, x = -1/3

Substituting x = -1/3 into the given polynomial:

`f(-1/3) = 3(-1/3)^4 - 5(-1/3)^3 - 71 (-1/3)^2 + 157(-1/3) + 60\\f(-1/3) = 0`

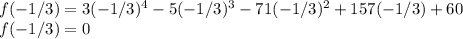
x + 1/3 is a factor