Question

Compare the time period of two simple pendulums of length 4m and 16m at a place.

Answer 1

the period of the 16 m pendulum is twice the period of the 4 m pendulum

Step-by-step explanation:

Recall that the period (T) of a pendulum of length (L) is defined as:

`T=2\,\pi\,\sqrt{ (L)/(g) }`

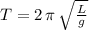
where "g" is the local acceleration of gravity.

SInce both pendulums are at the same place, "g" is the same for both, and when we compare the two periods, we get:

`T_1=2\,\pi\,\sqrt{(4)/(g) } \\T_2=2\,\pi\,\sqrt{(16)/(g) } \\ \\(T_2)/(T_1) =\sqrt{(16)/(4) } =2`

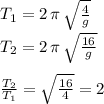
therefore the period of the 16 m pendulum is twice the period of the 4 m pendulum.