Question

Find the value of x in the triangle shown below​

Answer 1

46.4°

Explanation:

Apply sine formula:

`(sin \: a)/(a) = (sin \: b)/(b) = (sin \: c)/(c)`

`(sin \: a)/(a) = (sin \: c)/(c)`

Plug the values

`(sin \: (88))/(6.9) = (sin \: x)/(5)`

Apply cross product property

`5 \: sin \: (88) = 6.9 \: (sin \: x)`

`(5 \: sin \: (88))/(6.9) = sin \: x`

`x = {sin}^( - 1) ( (5 \: sin \:( 88))/(6.9) )`

`x = 46.4`

Hope this helps .....

Best regards!!!

Answer 2

x = 46.37 degrees

Explanation:

Using cosine rule

`c^2 = a^2+b^2-2abCosC`

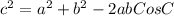
Where a = 5 , b = 6.9 , c = 5 and C = x (Unknown)

In the cosine rule, a and b are the sides containing the angle and c is the opposite side of the angle C

Plugging in the values:

`5^2 = 5^2+6.9^2-2(5)(6.9)Cos x`

=>
`25 = 25 + 47.62-2(34.5)Cosx`

=>
`25 = 72.61 - 69 Cos x`

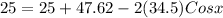
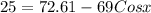
Subtracting 72.61 to both sides

=>
`25-72.61 = -69Cos x`

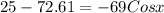
=> -47.61 = -69 Cos x

=> 47.61 = 69 Cos x

Dividing both sides by 69

=> Cos x = 0.69

Multiplying both sides by
`Cos^(-1)`

=> x =
`Cos^(-1)0. 69`

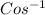
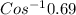
=> x = 46.37 degrees