Question

What is the area of the square adjacent to the third side of the triangle?

Answer 1

11 units²

Explanation:

If the triangle is right then area of square adjacent to the longest side is equal to sum of areas of squares adjacent to its other sides. (As in Pythagorean theorem)

So:

33 units² + ? = 44 units²

? = 44 units² - 33 units²

? = 11 units²

Answer 2

The area of the square adjacent to the third side of the triangle is 11 units²

Explanation:

We are given the area of two squares, one being 33 units² the other 44 units². A square is present with all sides being equal, and hence the length of the square present with an area of 33 units² say, should be x² = 33 - if x = the length of one side. Let's make it so that this side belongs to the side of the triangle, to our convenience,

x² = 33,

x =
`√(33)` .... this is the length of the square, but also a leg of the triangle. Let's calculate the length of the square present with an area of 44 units². This would also be the hypotenuse of the triangle.

x² = 44,

x =
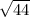`√(44)` .... applying pythagorean theorem we should receive the length of a side of the unknown square area. By taking this length to the power of two, we can calculate the square's area, and hence get our solution.

Let x = the length of the side of the unknown square's area -

`√((44))^2` =
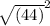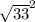`x^2` +
`√(33)^2`,

x =
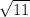`√(11)` ... And
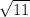`√(11)` squared is 11, making the area of this square 11 units².