Answer:
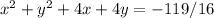
Explanation:
The axes x and y are calibrated in 0.25
If the circle is carefully considered, the radius r of the circle is:
r = -1.25 - (-2)
r = 0.75 units
The equation of a circle is given by:
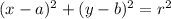
The center of the circle (a, b) = (-2, -2)
Substituting (a, b) = (-2, -2) and r = 0.75 into the given equation:
