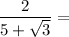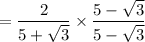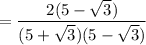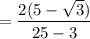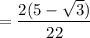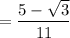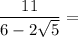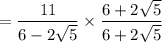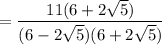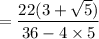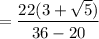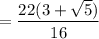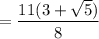Answer:
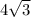
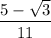
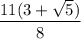
Explanation:
If you have a simple square root in the denominator, multiply the fraction by a fraction that is the root over the root.
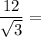
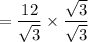
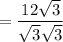
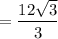
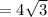
If you have a denominator consisting of a rational number plus a root, multiply the fraction by a fraction that is the denominator over the denominator in which you change only the sign outside the root.