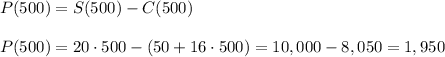Question

A high school wants to sell postage stamps with the school logo on them. The fundraising group have purchased 500 sheets of stamps at $16/sheet plus $50 to create the image. They plan to sell each sheet for $20. a) Write an equation that represents the cost of obtaining the stamps. b) Write an equation that represents the income from sales. c) For each equation, set up a table of values. d) Graph each equation on the same set of coordinate axis. e) What is the minimum number of sheets the group must sell so they don't lose any money? f) How much profit will they make if they sell 500 sheets?

Answer 1

a) Cost

`C(q) = 50+16q\\\\C(500)=50+16(500)=50+8,000=8,050`

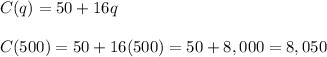
b) Sales income

`S(q)=20q\\\\S(500)=20\cdot 500 = 10,000`

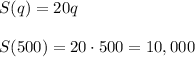
c) Table of values

`\left[\begin{array}{ccc}q&C(q)&S(q)\\0&50&0\\250&4,050&5,000\\500&8,050&10,000\end{array}\right]`

d) Attached

e) Breakeven point = 12.5 sheets

f) Profit at 550 sheets = $1,950

Explanation:

a) We have a fixed cost for the image, at $50.

We also have a variable cost of $16 a sheet.

The purchased quantity is 500 sheets.

Then, the cost function is:

`C(q) = 50+16q\\\\C(500)=50+16(500)=50+8,000=8,050`

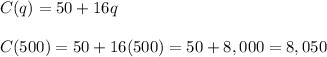
b) The price for each sheet is $20, so the income from sales are:

`S(q)=20q\\\\S(500)=20\cdot 500 = 10,000`

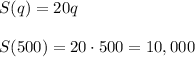
c) Table of values

`\left[\begin{array}{ccc}q&C(q)&S(q)\\0&50&0\\250&4,050&5,000\\500&8,050&10,000\end{array}\right]`

d) Attached

e) The minimum number of sheets the group must sell so they don't lose any money is the breakeven point (BEP) and can be calculated making the income sales equal to the cost:

`S(q)=C(q)\\\\20q=50+16q\\\\(20-16)q=50\\\\4q=50\\\\q=50/4=12.5`

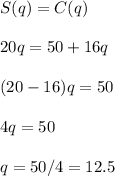
f) This profit can be calculated as the difference between the sales income and the cost:

`P(500)=S(500)-C(500)\\\\P(500)=20\cdot 500-(50+16\cdot 500)=10,000-8,050=1,950`