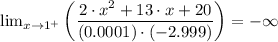Question

Evaluate each limit. Give exact answers.

Answer 1

Given that 1 and 4 are vertical asymtotes we have;

(a) -∞

(b) +∞

(c) +∞

(d) -∞

Explanation:

(a) For the function;

`\lim_(x\rightarrow 4^(-))\left ((2\cdot x^(2)+13\cdot x+20)/(x^(2)-5\cdot x+4) \right )`

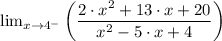
We have the denominator given by the expression, x² - 5·x + 4 which can be factorized as (x - 4)(x - 1)

Therefore, as the function approaches 4 from the left [lim (x → 4⁻)] gives;

`\lim_(x\rightarrow 4^(-))\left ((2\cdot x^(2)+13\cdot x+20)/((x - 1)\cdot (x - 4)) \right )`
`\lim_(x\rightarrow 4^(-))\left ((2\cdot x^(2)+13\cdot x+20)/((3.999 - 1)\cdot (3.999 - 4)) \right )`
`\lim_(x\rightarrow 4^(-))\left ((2\cdot x^(2)+13\cdot x+20)/((2.999)\cdot (-0.001)) \right )`
`=- \infty`

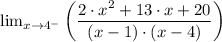
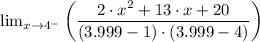
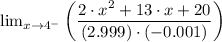
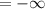
(b) Similarly, we have;

`\lim_(x\rightarrow 4^(+))\left ((2\cdot x^(2)+13\cdot x+20)/(x^(2)-5\cdot x+4) \right )`

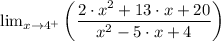
We have the denominator given by the expression, x² - 5·x + 4 which can be factorized as (x - 4)(x - 1)

Therefore, as the function approaches 4 from the right [lim (x → 4⁺)] gives;

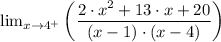
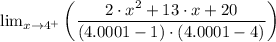
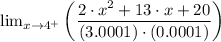
`\lim_(x\rightarrow 4^(+))\left ((2\cdot x^(2)+13\cdot x+20)/((x - 1)\cdot (x - 4)) \right )`
`\lim_(x\rightarrow 4^(+))\left ((2\cdot x^(2)+13\cdot x+20)/((4.0001 - 1)\cdot (4.0001 - 4)) \right )`
`\lim_(x\rightarrow 4^(+))\left ((2\cdot x^(2)+13\cdot x+20)/((3.0001)\cdot (0.0001)) \right )`
`= +\infty`

(c)

`\lim_(x\rightarrow 1^(-))\left ((2\cdot x^(2)+13\cdot x+20)/(x^(2)-5\cdot x+4) \right )`

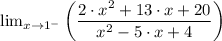
We have the denominator given by the expression, x² - 5·x + 4 which can be factorized as (x - 4)(x - 1)

Therefore, as the function approaches 1 from the left [lim (x → 1⁻)] gives;

`\lim_(x\rightarrow 1 ^(-))\left ((2\cdot x^(2)+13\cdot x+20)/((x - 1)\cdot (x - 4)) \right )`
`\lim_(x\rightarrow 1^(-))\left ((2\cdot x^(2)+13\cdot x+20)/((0.999 - 1)\cdot (0.999 - 4)) \right )`
`\lim_(x\rightarrow 4^(+))\left ((2\cdot x^(2)+13\cdot x+20)/((-0.001)\cdot (-3.001)) \right )`
`=+ \infty`

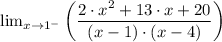
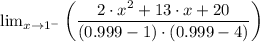
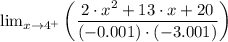
(d) As the function approaches 1 from the right [lim (x → 1⁺)]

We have;

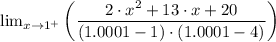`\lim_(x\rightarrow 1^(+))\left ((2\cdot x^(2)+13\cdot x+20)/((1.0001 - 1)\cdot (1.0001 - 4)) \right )`=
`\lim_(x\rightarrow 1^(+))\left ((2\cdot x^(2)+13\cdot x+20)/((0.0001)\cdot (-2.999)) \right ) =- \infty`