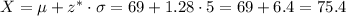Question

Please I need help with this question!

The weight of adult males in Boston are normally distributed with mean 69 kilograms and variance 25 kilograms.

I. what percentage of adult male in Boston weigh more than 72 kilograms?

ii. what must an adult male weigh in order to be among the heaviest 10% of the population?

Thank you in advance!​

Answer 1

I. 60%

II. 75.4 kg

Explanation:

We will use the z-scores and the standard normal distribution to answer this questions.

We have a normal distribution with mean 69 kg and variance 25 kg^2 (therefore, standard deviation of 5 kg).

I. What percentage of adult male in Boston weigh more than 72 kg?

We calculate the z-score for 72 kg and then calculate the associated probability:

`z=(X-\mu)/(\sigma)=(72-69)/(5)=(3)/(5)=0.6\\\\\\P(X>72)=P(z>0.6)=0.274`

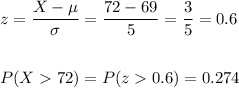
II. What must an adult male weigh in order to be among the heaviest 10% of the population?

We have to calculate tha z-score that satisfies:

`P(z>z^*)=0.1`

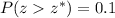
This happens for z=1.28 (see attachment).

Then, we can calculate the weight using this transformation:

`X=\mu+z^*\cdot\sigma=69+1.28\cdot 5=69+6.4=75.4`