Answer:
Ok, sabemos que la velocidad inicial de la pelota es 15m/s.
Desconocemos la posición inicial a la que es lanzada la pelota, pero vamos a suponer que es a una altura igual a cero, es decir, la pelota es lanzada al ras del suelo.
Una vez lanzada, la única fuerza actuando en la pelota es la gravitatoria, entonces la aceleración de la pelota es:
a = -g = -9.8m/s^2
El signo negativo es por que esta aceleración apunta hacia abajo.
Ahora, para la velocidad, necesitamos integrar sobre el tiempo.
v(t) = (-9.8m/s^2)*t + v0
donde v0 = 15m/s
v(t) = (-9.8m/s^2)*t + 15m/s.
De aca podemos obtener el tiempo en el que la pelota llega a la altura máxima, que es el punto donde la velocidad es igual a cero.
0 = (-9.8m/s^2)*t + 15m/s.
t = (15/9.8)s = 1.53 s
Ahora, para la ecuación de la posición integramos la ecuación de la velocidad sobre el tiempo:
p(t) = (1/2)(-9.8m/s^2)*t^2 + 15m/s*t + p0
donde p0 es la pocision inicial, pero arriba dijimos que era igual a cero, entonces la ecuación queda:
p(t) = (-4.5m/s^2)*t^2 + 15m/s*t
ahora reemplazamos t por el tiempo que encontramos antes, y descubrimos que:
p(1.53s) = (-4.5m/s^2)*(1.53s)^2 + 15m/s*1.53s = 12.41m
La máxima altura que alcanza la pelota es 12.41 metros arriba del punto desde el que se la lanzo.
Ahora, el tiempo total que esta en el aire puede ser calculado de tal forma que la posición vuelva a ser cero, es decir, la pelota llega a la misma altura desde la que fue lanzada inicialmente (y es agarrada por la persona, podemos suponer)
Entonces:
p(t) = 0 = (-4.5m/s^2)*t^2 + 15m/s*t
Ahora resolvemos la eq cuadrática, usando la eq. de Bhaskara:
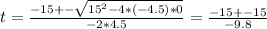
Entonces las soluciones son:
t = (-15 + 15)/-9.8 = 0s
t = (-15 - 15)/-9.8 = 3.06s
Tomamos la segunda solución, ya que la primera corresponde al tiempo inicial.
Entonces concluimos con que la pelota estuvo 3.06 segundos en el aire.