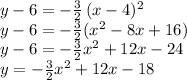Question

a parabola has an x-intercept at 2, its axis of symmetry is the line x=4, and the y-coordinate of its vertex is 6. Determine the equation of the parabola.

Answer 1

The standard equation of the parabola is:

`y=-(3)/(2)x^2+12x-18`

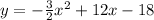
Explanation:

An x intercept of 2 means that the point (2, 0) is in the graph of the parabola.

We can also write the general expression for the parabola in vertex form, since we can use the information on the coordinates of the vertex: (4, 6) - recall that the axis of symmetry of the parabola goes through the parabola's vertex, so the x-value of the vertex must be x=4.

`y-y_(vertex)=a\,(x-x_(vertex))^2\\y-6=a\,(x-4)^2`

Now we can find the value of the parameter "a" by using the extra information about the point (2, 0) at which the parabola intercepts the x-axis:

`y-6=a\,(x-4)^2\\0-6=a\,(2-4)^2\\-6=a\,4\\a=-(6)/(4) =-(3)/(2)`

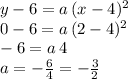
Then the equation of the parabola becomes:

`y-6=-(3)/(2) \,(x-4)^2\\y-6=-(3)/(2) (x^2-8x+16)\\y-6=-(3)/(2)x^2+12x-24\\y=-(3)/(2)x^2+12x-18`