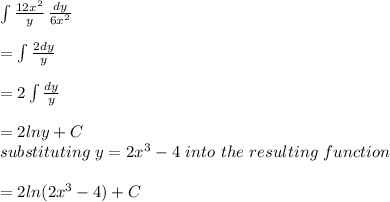Question

How would you solve this problem?

Answer 1

a) 6x²/2x³-4

b)
`2ln (2x^3-4)+ C`

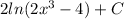
Explanation:

a) Given the ln(2x³-4). We will use the chain rule in differentiating the function

If y = ln(2x³-4);

u = 2x³-4; du/dx = 3(2)x³⁻¹

du/dx = 6x²

y = ln u; dy/du = 1/u

According to chain rule, dy/dx = dy/dy*du/dx

dy/dx = 1/u * 6x²

dy/dx = 1/2x³-4 * 6x²

dy/dx = 6x²/2x³-4

Hence, the derivative of the given function is 6x²/2x³-4

b) Given an integral function
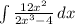`\int\limits {(12x^2)/(2x^3-4) } \, dx`, the integral problem can be solved using integration by substitution method as shown below;

From the question, let y = 2x³-4... 1, dy/dx = 6x²

dx = dy/6x² ... 2

Substituting equation 1 and 2 into the question given;

`\int\limits {(12x^2)/(y) } \,(dy)/(6x^2) \\\\= \int\limits {(2dy)/(y) } \\\\= 2 \int\limits {(dy)/(y) }\\\\= 2lny + C\\substituting\ y = 2x^3-4\ into\ the \ resulting\ function\\\\= 2ln (2x^3-4)+ C`