Question

If $y^2= 36$, what is the greatest possible value of $y^3$?

Answer 1

216

Explanation:

If y² = 36, then y is 6 or -6. When y = 6, we have y³ = 6³ = 216. When y = -6, we have y³ = (-6)³ = -216. The greatest possible value of y³ is 216.

Answer 2

The greatest possible value of
`y^3=216`

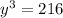
Explanation:

We have the statement
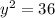`y^2=36`, and we have to find the greatest possible value of
`y^3`, first we need to find the value of y.

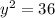`y^2=36`, to get the y by itself on the left side, we need to take the square root of both sides.
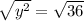`√(y^2) =√(36)` The square root of
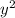`y^2` is y, because y*y =
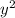`y^2`, and the square root of 36 is 6 or -6.

We now need to find the greatest value of
`y^3`. When we plug in 6 to
`y^3`, we get positive 216, and when we plug in -6, we get -216. We need to find the greatest possible value, so in this case we compare 216 and -216, 216 is greater than -216, so the answer would be positive 216.