Answer:
tanФ = 2.6363636
Explanation:
To find the tangent of the angle in-between the lines we will follow the steps below:
We are going to use the formula;
tanФ = |m₂ - m₁ / 1 + m₁m₂|
We can get the slope m₁ from the first equation
2x+3y–5=0
we will re-arrange it in the form y=mx + c
3y = -2x + 5
Divide through by 3
y = -
 x +
x +
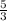
comparing the above equation with y=mx + c
m₁ = -

We will proceed to find the second slope m₂ using the second equation
5x=7y+3
we will re-arrange it in the form y=mx + c
7y = 5x -3
divide through by 7
y =
 x -
x -

comparing the above with y=mx + x
m₂ =

we can now go ahead and substitute into the formula
tanФ = |m₂ - m₁ / 1 + m₁m₂|
tanФ = |
 - (-
- (-
 ) / 1 + (-
) / 1 + (-
 ₁)(
₁)(
 )|
)|
tanФ = |
 +
+
 / 1 -
/ 1 -
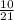 |
|
tanФ = |
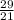 /
/
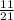 |
|
tanФ = |
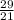 ×
×
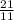 |
|
21 will cancel-out 21
tanФ =

tanФ = 2.636363