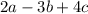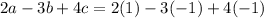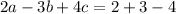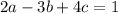Answer:
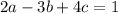
Explanation:
Given
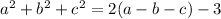
Required
Determine
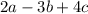
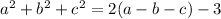
Open bracket
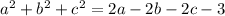
Equate the equation to 0
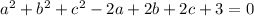
Express 3 as 1 + 1 + 1
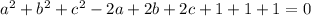
Collect like terms
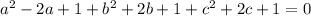
Group each terms
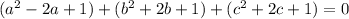
Factorize (starting with the first bracket)
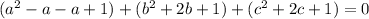
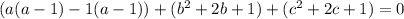
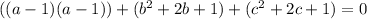
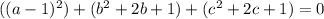
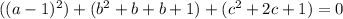
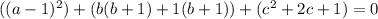
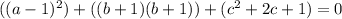
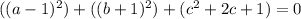
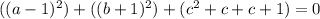
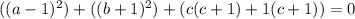
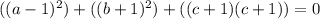
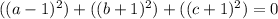
Express 0 as 0 + 0 + 0
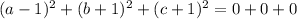
By comparison
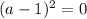
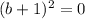
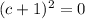
Solving for
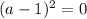
Take square root of both sides
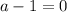
Add 1 to both sides
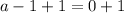
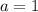
Solving for
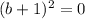
Take square root of both sides
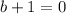
Subtract 1 from both sides
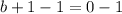
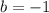
Solving for
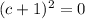
Take square root of both sides
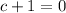
Subtract 1 from both sides
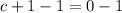
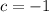
Substitute the values of a, b and c in