Answer:
The owner needs 195 meters of wire
Explanation:
If the lot is squared shaped, then its area is given by the formula:
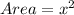
where x is the side of the square. Then considering the value they provide for the surface, each side must be of length:
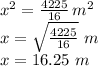
Then the perimeter around this square lot is four times that side length:
Perimeter = 4 (16.25 m) = 65 m
and since the owner wants three rows of wire, the total length of wire needed is:
3 (65 m) = 195 m