Question

Rectangular field has a total perimeter of 128 feet. The width is

A
24 feet less than the length. What are the dimensions of the field?

Answer 1

`\boxed{l=44 \: \mathrm{feet}, \: \: w=20 \: \mathrm{feet}}`

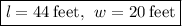
Explanation:

The width (w) = l - 24

The length (l) = l

The perimeter (P) = 128

The shape is a rectangle. Use the formula for the perimeter of a rectangle.

P = 2w + 2l

Plug in the values.

128 = 2(l - 24) + 2l

Solve for l.

Expand brackets.

128 = 2l - 48 + 2l

Combine like terms

128 = 4l - 48

Add 48 on both sides.

176 = 4l

Divide both sides by 4.

44 = l

Apply formula again.

P = 2l + 2w

Solve for w.

Subtract 2w and P on both sides.

-2w = 2l - P

Divide both sides by -2.

w = -l + P/2

Plug in the values for l and P, solve for w.

w = -(44) + 128/2

w = -44 + 64

w = 20

The length is 44 feet.

The width is 20 feet.

Answer 2

l = 44 ft

w = 20 ft

Explanation:

Perimeter is

P = 2 ( l+w)

The width is

w = l -24

We know the perimeter is 128 and substituting into the equation for perimeter

128 = 2 ( l + l-24)

128 = 2 ( 2l -24)

Divide by 2

128/2 = 2/2 ( 2l-24)

64 = 2l - 24

Add 24 t o each sdie

64+24 = 2l

88 = 2l

Divide by 2

44 =l

The length is 44

Now find w

w = l - 24

w = 44-24

w = 20