Question

Factorize a² +3ab - 5ab - 15b².

Answer 1

`\boxed{\sf (a + 3b)(a - 5b)}`

Explanation:

`\sf Factor \: the \: following: \\ \sf \implies {a}^(2) + 3ab - 5ab - 15 {b}^(2) \\ \\ \sf Grouping \: like \: terms, \\ \sf {a}^(2) + 3ab - 5ab - 15 {b}^(2) = {a}^(2) + (3ab - 5ab) - 15 {b}^(2) : \\ \sf \implies {a}^(2) + (3ab - 5ab) - 15 {b}^(2) \\ \\ \sf 3ab - 5ab = - 2ab : \\ \sf \implies {a}^(2) - 2ab - 15 {b}^(2) \\ \\ \sf The \: factors \: of \: - 15 \: that \: sum \: to \: - 2 \: are \: 3 \: and \: - 5. \\ \\ \sf So, \\ \sf \implies {a}^(2) + (3 - 5)ab - 15 {b}^(2) \\ \\ \sf \implies {a}^(2) + 3ab - 5ab - 15 {b}^(2) \\ \\ \sf \implies a(a + 3b) - 5b(a + 3b) \\ \\ \sf \implies (a + 3b)(a - 5b)`

Answer 2

`a^2+3\,a\,b-5\,a\,b-15\,b^2=(a-5\,b)\,(a+3\,b)`

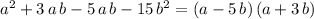
Explanation:

Work via factoring by groups:

!) re arrange the terms as follows:

`a^2-5ab+3ab-15b^2`

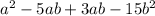
then extract the common factor for the first two terms (a), and separately the common factors for the last two terms (3 b):

`a^2-5ab+3ab-15b^2\\a\,(a-5\,b)+3\,b\,(a-5\,b)`

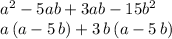
Now notice that the binomial factor (a-5 b) is in both expressions, so extract it:

`a\,(a-5\,b)+3\,b\,(a-5\,b)\\(a-5\,b)\,(a+3\,b)`

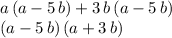
which is the final factorization.