Answer:
f(x) = 3x⁴ -
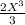 - 17x +
- 17x +

Explanation:
To find f'(x), we will follow the steps below:
We will start by integrating both-side of the equation
∫f'(x) = ∫(12x^3 - 2x^2 - 17)dx
f(x) = 3x⁴ -
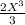 - 17x + C
- 17x + C
Then we go ahead and find C
f(1) = 8
so we will replace x by 1 in the above equation and solve for c
f(1) = 3(1)⁴ -
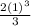 - 17(1) + C
- 17(1) + C
8 = 3 -
 - 17 + C
- 17 + C
C =8 - 3 + 17 +

C = 22 +

C =
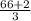
C =

f(x) = 3x⁴ -
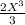 - 17x +
- 17x +
