Answer:
For this case we know that at the starting year 2000 the population was 9 billion and we also know that increasing with a double time of 20 years so we can set up the following model:
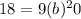
And if we solve for b we got:

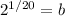
And then the model would be:
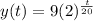
Where y is on billions and t the time in years since 2000.
And for this equation is possible to find the population any year after 2000
Explanation:
For this case we know that at the starting year 2000 the population was 9 billion and we also know that increasing with a double time of 20 years so we can set up the following model:
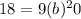
And if we solve for b we got:

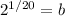
And then the model would be:
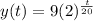
Where y is on billions and t the time in years since 2000.
And for this equation is possible to find the population any year after 2000