Question

find the value of a and b for which the system of equations has infinitely many solutions : 2x + 3y = 7 ; (a-b)x + (a+b)y = 3a + b - 2​

Answer 1

a= 5 and b=1

Explanation:

To solve, we will follow the steps below:

2x + 3y = 7

(a-b)x + (a+b)y = 3a + b - 2​

We should note that since it has infinitely many solutions then,

`(a_(1) )/(a_(2) ) = (b_(1) )/(b_(2) ) = (c_(1) )/(c_(2) )`

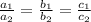
Hence

2/a-b = 3/a+b = 7/3a +b-2

2/a-b = 3/a+b

cross-multiply

3(a-b) = 2( a+b)

open the bracket

3a - 3b = 2a + 2b

collect like term

3a - 2a = 2b + 3b

a = 5b -------------------------------------------(1)

Similarly

3/a+b = 7/3a +b-2

cross-multiply

7(a+b) = 3(3a+b -2)

7a + 7b = 9a + 3b -6

take all the variables to the left-hand side of the equation

7a - 9a+ 7b-3b = -6

-2a + 4b = -6 ---------------------------------(2)

but a = 5b

substitute a= 5b in equation (2) and solve for b

-2(5) + 4b = -6

-10 + 4b = -6

add 10 to both-side of the equation

-10 + 10+ 4b = -6+10

4b = 4

divide both-side of the equation by 4

b = 1

substitute b= 1 in equation (1)

a = 5b

a =5(1)

a=5

Therefore, a= 5 and b=1