Question

A study was conducted to measure the effectiveness of hypnotism in reducing pain. The measurements are centimeters on a pain scale before and after hypnosis. Assume that the paired sample data are simple random samples and that the differences have a distribution that is approximately normal. Does hypnotism appear to be effective in reducing pain? In this example, μd is the mean value of the differences d for the population of all pairs of data, where each individual difference d is defined as the difference in the measurements on a pain scale before and after hypnosis. What is the test statistic for this hypothesis test?

Answer 1

Explanation:

Hello!

This is an example of a pared sample test, the experiment is based on two dependent variables:

X₁: centimeters on a pain scale before hypnosis

X₂: centimeters on a pain scale after hypnosis

Out of these two variables a new variable is determined Xd= X₁-X₂

If the variables have an approximate normal distribution then the variable resulting from their difference will also have an approximate normal distribution.

The claim is that "hypnosis reduced the pain" if so you'd expect the population mean of the difference to be less than zero, symbolically: μd<0

The statistic for this test is a paired sample t test:

`t= \frac{\frac{}{X_d} - Mu_d}{Sd} ~t_(n-1)`

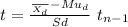
To calculate the sample mean and variance you have to calculate the difference between the pairs first.

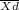`\frac{}{Xd}`= ∑Dif/n

`S_d^2= (1)/(n-1) [sumDif^2- ((sumDif)^2)/(n) ]`

∑Dif= 6.4

∑Dif²= 12.64

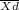`\frac{}{Xd}`= 6.4/5= 1.28

`S_d^2= (1)/(4) [12.64- ((6.4)^2)/(5) ]= 1.112`

Sd= 1.05

`t_(H_0)= \frac{\frac{}{Xd}-Mu_d }{Sd} = (1.28-0)/(1.05) = 1.219= 1.22`

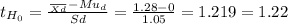
I hope this helps!