Question

5.

Find the equation of the circle tangential to the line 3x-4y+1=0 and with
centre at (4,7).
20​

Answer 1

Answer: (x - 4)² + (y - 7)² = 9

Step-by-step explanation:

The equation of a circle is: (x - h)² + (y - k)² = r² where

• (h, k) is the center
• r is the radius

Given: (h, k) = (4, 7)

Find the intersection of the given equation and the perpendicular passing through (4, 7).

3x - 4y = -1

-4y = -3x - 1

`y=(3)/(4)x-1`

`m=(3)/(4)` -->
`m_(\perp)=-(4)/(3)`

`y-y_1=m_(\perp)(x-x_1)\\\\y-7=-(4)/(3)(x-4)\\\\\\y=-(4)/(3)x+(16)/(3)+7\\\\\\y=-(4)/(3)x+(37)/(3)`

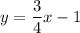
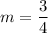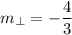
Use substitution to find the point of intersection:

`x=(29)/(5)=5.8,\qquad y=(23)/(5)=4.6`

Use the distance formula to find the distance from (4, 7) to (5.8, 4.6) = radius

`r=√((5.8-4)^2+(4.6-7)^2)\\\\r=√(3.24+5.76)\\\\r=\sqrt9\\\\r=3`

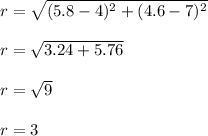
Input h = 4, k = 7, and r = 3 into the circle equation:

(x - 4)² + (y - 7)² = 3²

(x - 4)² + (y - 7)² = 9