Answer:

Explanation:
Hello,
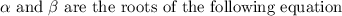
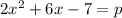
It means that
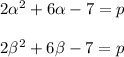
And we know that
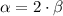
So we got two equations

For
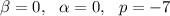
For
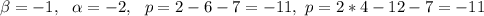
I assume that we are after two different roots so the solution for p is p=-11
b)

So a quadratic equation with the expected roots is
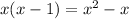
Hope this helps.
Do not hesitate if you need further explanation.
Thank you