Question

Evaluate the series

Answer 1

the value of the series;

`\sum_(k=1)^(6)(25-k^2) = 59`

C) 59

Explanation:

Recall that;

`\sum_(1)^(n)a_n = a_1+a_2+...+a_n\\`

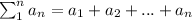
Therefore, we can evaluate the series;

`\sum_(k=1)^(6)(25-k^2)`

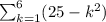
by summing the values of the series within that interval.

the values of the series are evaluated by substituting the corresponding values of k into the equation.

`\sum_(k=1)^(6)(25-k^2) =(25-1^2)+(25-2^2)+(25-3^2)+(25-4^2)+(25-5^2)+(25-6^2)\\\sum_(k=1)^(6)(25-k^2) =(25-1)+(25-4)+(25-9)+(25-16)+(25-25)+(25-36)\\\sum_(k=1)^(6)(25-k^2) =24+21+16+9+0+(-11)\\\sum_(k=1)^(6)(25-k^2) = 59\\`

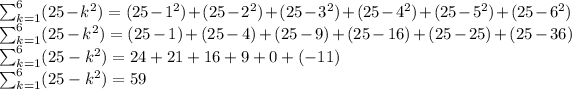
So, the value of the series;

`\sum_(k=1)^(6)(25-k^2) = 59`