Answer:
The plane is 388 miles far from the airport.
Explanation:
We know that, the angle between southeast and south directions is
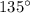 .
.
The plane travels as per the triangle as shown in the attached image.
A is the location of airport.
First it travels for 210 miles southeast from A to B and then 210 miles south from B to C.
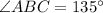
To find:
Side AC = ?
Solution:
As we can see, the
 is an isosceles triangle with sides AB = BC = 210 miles.
is an isosceles triangle with sides AB = BC = 210 miles.
So, we can say that the angles opposite to the equal angles in a triangle are also equal.
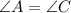
And sum of all three angles of a triangle is equal to
 .
.

Now, we can use Sine Rule:
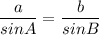
a, b are the sides opposite to the angles
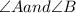 respectively.
respectively.
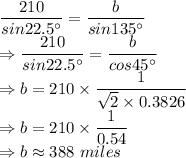
So, the answer is:
The plane is 388 miles far from the airport.