Question

When shopping for accessories for her action camera, Giana found an advertisement for a replacement battery. The advertisement includes

the given graph of a function to represent the charge remaining in the battery after streaming x hours of video.

Answer 1

The x-intercept for the function is (8,0).

The equation of the function is 25x + 2y = 200.

The equation of the function is y =-25/2 x + 100.

Explanation:

Answer 2

The correct options are;

The equation of the function is 2·y = -25·x + 200

The equation of the function is y = -25/2·x + 100

The x-intercept of the function is (8, 0)

Explanation:

From the graph of the function, the y-intercept is observed at (0, 100), the x-intercept occurs at (8, 0)

Therefore, we have the slope, m given by the following relation

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

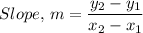
Where:

y₁ = 100

x₁ = 0

y₂ = 0

x₂ = 8

Which gives;

`m =(0-100)/(8-0) = -12.5`

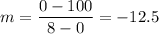
The equation in slope can be found as follows

y - 100 = -12.5×(x - 0)

y = -12.5·x + 100 = -25/2·x + 100

Multiplying by 2 gives;

2·y = -25·x + 200

25·x + 2·y = 200

Therefore, the correct options are;

The equation of the function is 2·y = -25·x + 200

The equation of the function is y = -25/2·x + 100

The x-intercept of the function is (8, 0).